Homotecia

La Homotecia es una transformación geométrica plana, en la cual los puntos relacionados o transformados se denominan homotéticos, y cumplen las siguientes condiciones:

• Los puntos homotéticos están alineados con un tercero fijo llamado centro de la Homotecia (O).
• La relación entre los segmentos definidos por este centro y los puntos transformado y original es una constante denominada razón de la homotecia (k).

Propiedades

Dos figuras homotéticas guardan relación de semejanza.

El centro de la Homotecia es invariante, y las rectas que pasan por el centro de la Homotecia también lo son, aunque no lo son por puntos (los puntos no son dobles).

En una Homotecia pueden darse los siguientes casos:

Si la constante k es mayor que 0, la Homotecia se denomina directa, y en ella los puntos homotéticos están ambos al mismo lado del centro de la Homotecia.

• Si la constate k es menor que 0, la Homotecia se denomina inversa, y en ella los puntos homotéticos están en lados diferentes con respecto al centro de la Homotecia.
• Si la constante k es 1, la figura homotética coincide con la original, y la transformación se denomina Función Identidad.
• Si la constante k es -1, la Homotecia se convierte en una Simetría Central (ver capítulo 2.4).
• Si el valor absoluto de la constante k es mayor que 1, la Homotecia produce un aumento de tamaño (la figura final es mayor que la original).
• Si el valor absoluto de la constante k es menor que 1, la Homotecia produce una disminución de tamaño (la figura final es menor que la original).

Dos rectas homotéticas siempre son paralelas, y la razón de longitud de dos segmentos homotéticos es igual a la razón de la homotecia (k).

La Homotecia es una transformación plana reversible, esto es, si aplicamos una homotecia a una figura y después aplicamos una segunda homotecia de igual centro y con igual razón, pero de diferente signo, obtenemos la figura original.

Una Homotecia de centro impropio (en el infinito) es una Traslación.

Homotecia de circunferencias

La homotética de una circunferencia es otra circunferencia cuyo centro es el homotético del centro de la primera, y cuyos puntos son homotéticos uno a uno.

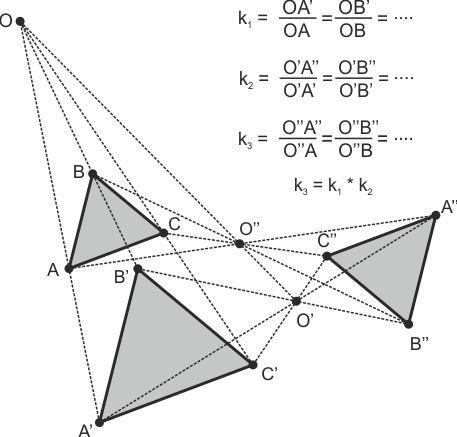
Producto de dos Homotecias

El producto de dos homotecias es otra homotecia, cuyo centro está alineado con los centros de las dos transformaciones originales (aunque esta homotecia final puede resultar de centro impropio, convirtiéndose en una traslación) y cuya razón es el producto de las dos razones.

Dominio e Imagen de una Función

Una función es una relación (pero con algunos ingredientes
adicionales). Por lo tanto están definidos los conceptos de dominio e imagen de una función.

Definición de Relación (Matemáticas).

Dados dos conjuntos A y B, una relación R entre A y B es un subconjunto del producto cartesiano AXB.

Polígonos Regulares

Definición: Un polígono regular es una figura plana (bidimensional) formada por una linea poligonal cerrada y todos los puntos interiores a ella. Tienen la característica de que todos sus lados y ángulos son congruentes (iguales).

Elementos de un Polígono Regular:

8) Datos Curioso sobre Matemáticas

1) Símbolo de igualdad:
Las dos rayas = que indican igualdad las empezó a utilizar un matemático inglés llamado Robert Recorde que vivió hace más de cuatrocientos años. En uno de sus libros cuenta que eligió ese signo porque “dos cosas no pueden ser más iguales que dos rectas paralelas”


2) Fibonacci:
Si cuentas las escamas de una piña, observarás sorprendido que aparecen en espiral alrededor del vértice en número igual a los términos de la sucesión de Fibonacci 

3) Sistema Decimal:
El hecho de que tengamos diez dedos en las manos y diez dedos en los pies, ha determinado la adopción del sistema decimal de numeración; aunque con el correr de los siglos se han propuesto y utilizado otros sistemas.


4) Sistema Sexadecimal:

El sistema sexagesimal (base 60) fue creado por los babilonios hacia el año 200 antes de Cristo y se usa todavía para medir el tiempo y los ángulos.


5) Número Cero:

La palabra cero deriva probablemente de “zephirum”, forma latinizada del árabe “sifr” que es, a su vez, una traducción de la palabra hindú “sunya” que significa vacío o nada.

6) Probabilidad
La teoría de probabilidad tiene su origen en los juegos de azar. Hacia 1650, en Francia, un jugador llamado De Mére consultó al matemático Blaise Pascal algunas cuestiones relacionadas con el juego de dados. Pascal mantuvo correspondencia con Fermat, Huygens y Bernoulli. Gracias a todos ellos, la teoría de la probabilidad pasó de ser una mera colección de problemas aislados, relativos a algunos juegos, a ser un sector importante de las matemáticas.


7) Geometría

La geometría (medición de tierra) se inició, como ciencia, en el antiguo Egipto y en Babilonia por la necesidad de realizar mediciones terrestres.


8) El símbolo de coma

El primero en usar la coma para separar la parte decimal de la fraccionaria fue el astrónomo italiano Giovanni Magini. La invención de los logaritmos generalizó el uso de los números decimales y el escocés John Napier, inventor de los logaritmos neperianos, recomendó en 1617 el uso del punto; el caos siguió durante todo el siglo XVIII aunque al final solo quedaron en competencia el punto y la coma. En el continente europeo el asunto se resolvió en 1698, cuando Leibnitz, propuso usar el punto como símbolo de multiplicación (“en lugar del signo x, que se confunde con x, la incógnita”); quedó así la coma para separar la parte decimal del número. En Inglaterra, sin embargo, donde se habían cerrado las puertas al alemán Leibnitz, se siguió utilizando el símbolo x para la multiplicación y el punto para separar los decimales. En España y América también se usó, y se sigue aceptando, la coma elevada.

Inyectividad, sobreyectividad y biyectividad

La Inyectividad, sobreyectividad y biyectividad  dan información sobre el comportamiento de una Funciòn

Puedes entender una función como una manera de conectar elementos de un conjunto "A" a los de otro conjunto "B":

"Inyectividad" significa que cada elemento de "B" tiene como mucho uno de "A" al que corresponde (pero esto no nos dice que todos los elementos de "B" tengan alguno en "A").

"Sobreyectividad" significa que cada elemento de "B" tiene por lo menos uno de "A" (a lo mejor más de uno).

"Biyectividad" significa inyectividad y sobreyectividad a la vez. Así que hay una correspondencia perfecta "uno a uno" entre los elementos de los dos conjuntos.

Definiciones formales

Inyectividad

Una función f es inyectiva si, cuando f(x) = f(y), x = y.

Ejemplo: f(x) = x² del conjunto de los números naturales  a  es una función inyectiva.

(Pero f(x) = x² no es inyectiva cuando es desde el conjunto de enteros  (esto incluye números negativos) porque tienes por ejemplo

• f(2) = 4 y
• f(-2) = 4)

Sobreyectividad (o también "epiyectividad")

Una función f (de un conjunto A a otro B) es sobreyectiva si para cada y en B, existe por lo menos un x en Aque cumple f(x) = y, en otras palabras f es sobreyectiva si y sólo si f(A) = B.

Así que cada elemento de la imagen corresponde con un elemento del dominio por lo menos.

Ejemplo: la función f(x) = 2x del conjunto de los números naturales  al de los números pares no negativos es sobreyectiva.

Sin embargo, f(x) = 2x del conjunto de los números naturales  a  no es sobreyectiva, porque, por ejemplo, ningún elemento de  va al 3 por esta función.

Biyectividad

Una función f (del conjunto A al B) es biyectiva si, para cada y en B, hay exactamente un x en A que cumple que f(x) = y

Alternativamente, f es biyectiva si es a la vez inyectiva y sobreyectiva.

Ejemplo: La función f(x) = x² del conjunto de números reales positivos al mismo conjunto es inyectiva y sobreyectiva. Por lo tanto es biyectiva.

(Pero no desde el conjunto de todos los números reales porque podrías tener por ejemplo

• f(2)=4 y
• f(-2)=4)

Personajes Históricos en Matemática: David Hilbert

(Wehlan, actual Alemania, 1862 - Gotinga, id., 1943) Matemático alemán. Su padre era juez, y fue destinado al poco de su nacimiento a Königsberg, donde David recibió su educación y en cuya universidad inició los estudios de matemáticas. Estudió también en las universidades de Heidelberg y de Berlín, asistiendo en esta última a los cursos de Weierstrass, Kummer, Helmholtz y Kronecker.

David Hilbert

A finales de 1884 se doctoró en Königsberg, poco antes de que hiciera lo propio su amigo Hermann Minkowski. La tesis de Hilbert trataba de los invariantes algebraicos, un tema que le propuso su joven profesor F. Lindemann, quien dos años antes había demostrado que «pi» es un número trascendente.

Viajó después a Leipzig, donde asistió a las clases de Felix Klein, y a París, donde conoció a Henri Poincaré, Camille Jordan y Charles Hermite. De regreso a Königsberg, en 1886 inició allí su carrera académica como privatdozent; siete años más tarde, cuando Lindemann marchó a Berlín, Hilbert accedió al cargo de profesor ordinario por recomendación de Klein, por entonces profesor en Gotinga; a esta universidad se incorporó también Hilbert en 1895, de nuevo por intervención de Klein, y en ella desarrolló el resto de su carrera profesional.

En Gotinga centró su atención en la geometría, tratando de plasmar en ese nuevo interés una idea que alimentaba desde mucho antes: lo importante no es la naturaleza de los objetos geométricos, sino la de sus interrelaciones. En su obra de 1899, dedicada a proporcionar a la geometría euclidiana una fundamentación estrictamente axiomática y que ha ejercido una gran influencia sobre el desarrollo de la matemática en el siglo XX, realizó el primer esfuerzo sistemático y global para hacer extensivo a la geometría el carácter puramente formal que ya habían adquirido la aritmética y el análisis matemático.

En el Congreso Internacional de Matemáticos celebrado en París en 1900, Hilbert presentó una lista de veintitrés problemas que a la sazón no habían sido resueltos todavía; a su juicio, las probables líneas de desarrollo que iba a seguir la matemática del siglo XX habrían de estar en buena medida vinculadas a la resolución de dichas cuestiones. Sus trabajos posteriores desembocaron en la concepción de los espacios de infinitas dimensiones llamados espacios de Hilbert, base del moderno análisis funcional.

A partir del año 1904, empezó a desarrollar un programa para dotar de una base axiomática a la lógica, la aritmética y la teoría de conjuntos, con el objetivo último de axiomatizar toda la matemática. Aunque su propósito de demostrar la consistencia de la aritmética había de verse frustrado por los resultados posteriores (1931) obtenidos por Kurt Gödel, el programa de formalización de Hilbert contribuyó al desarrollo de la llamada metamatemática, como método para establecer la consistencia de cualquier sistema formal.